다양한 유체를 멀리 이송하기 위해 배관이 사용됩니다. 배관 내의 유체의 길을 「관로」라고 합니다.
관로 내를 유체가 흐를 때, 유체의 점성에 의한 마찰로 인해 압력 손실이 발생합니다.
이 때문에, 액체이면 펌프, 기체이면 송풍기나 압축기 등의 유체 기계를 사용하여, 압력 손실을 보충할 뿐인 압력 에너지를 유체에 가할 필요가 있습니다.
목차
1. 층류, 난류, 레이놀즈 수
2. 직관에서의 마찰 손실
《층류의 경우》
《난류의 경우》
3. 관로 단면이 비원형인 경우
4. 다양한 관로 요소의 손실
(1) 관로의 급 수축
(2) 탱크에서 관로로의 입구
(3) 관로의 급 확대
(4) 관로에서 저수지나 탱크로의 유출
(5) 굴곡부 (구브러진 부분)
(6) 밸브
1. 층류(層流)、난류(乱流)、레이놀즈 수
층류, 난류, 레이놀즈 수란? (간단하게 알아보겠습니다
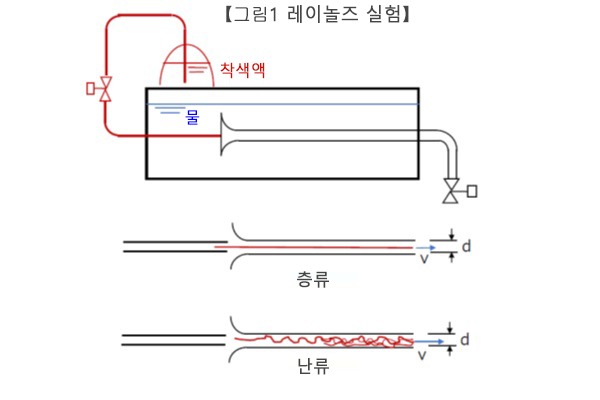
단면 형상이 원의 관로(원관) 내에 비압축성 유체를 흘리는 경우, 유속이 느릴 때, 흐름은 흐트러지지 않고 똑바로 직선형의 모양을 그려 흐릅니다. 이러한 흐름을 「층류」「層流」라고 합니다.
유속이 커지면, 흐름은 흐름 방향 이외의 속도 성분을 가지게 되어, 소용돌이를 발생하여 흐트러진 상태가 됩니다. 이러한 흐름을 「난류」「乱流」라고 합니다.
1883년 레이놀즈는, 아래 그림과 같은 흐름의 가시가 장치(可視可装置)를 고안 제작하여, 수온, 관경, 유속을 바꾸어 실험을 실시해, 층류로부터 난류로 변화하는 현상(천이遷移)은, 다음식으로 나타내는 무차원수 Re에 의해 판별되는 것을 발견했습니다.
Re = vd/ν ・・・(1)
여기서, v: 유속(m/s), d: 관내경(m), v: 동점도 動粘度(m2/s)
이 무차원수 Re를 「레이놀즈수」라고 합니다.
레이놀즈 수는 흐름의 관성력과 점성력의 비율을 나타내는 수치입니다.
유속이 작으면 점성력이 지배적이 되어 흐름은 층류가 되어 레이놀즈수는 작아집니다. 유속이 커지면 관성력이 지배적이 되어 흐름은 난류가 되어 레이놀즈수는 커집니다.
층류로부터 난류로의 전이가 일어날 때의 레이놀즈수를 임계 레이놀즈수 Rec라고 하며, 원관내의 흐름에 있어서 Rec는 약 2320이 됩니다.
실제로는, 층류로부터 난류로의 전이와 난류에서 층류로의 전이에서 Rec는 다르고, 입구부의 유동 상태 등에도 영향을 받고, 층류, 난류의 전이 영역은 2100<Rec <4000 정도의 범위가 됩니다.
2. 직관에서의 마찰 손실
내경 d(m), 길이 L(m)의 직관내를 유속 v(m/s)로 유체가 흐를 때 생기는 손실 헤드 hL(m)을 다음 식으로 계산할 수 있습니다.
hL=λ(L/d)(v2/2g) ・・・(2)
[g: 중력 가속도(m/s2), λ: 관 마찰 계수(무차원)]
(2)식을, 다르시-·와이스바흐의 식이라고 하며, 층류·난류에 관계없이, 점성에 의한 마찰 손실을 계산하는 공식으로서 적용할 수 있습니다.
관 마찰 계수 λ는, 흐름이 층류인 경우와 난류인 경우에 따라 다릅니다.
《층류의 경우》
λ=64/ Re ・・・(3)
위 식으로 표시되며, λ는 레이놀즈 수 Re에 반비례하는 함수가 됩니다.
《난류의 경우》
벽면이 매끄러운 경우에는, λ가 Re의 함수가 되는 몇 가지 실험식이 있습니다.
다만 적용 가능한 Re 범위가 있으므로 주의가 필요합니다.
① 브라지우스의 식(Re =3×103~1×105)
λ = 0.3164 / Re 0.25 ・・・(4)-1
② 니크라제 식(Re =1 × 106~3 × 106)
λ=0.0032+0.221 Re-0.237 ・・・(4)-2
③ 칼만・플란틀 의 식
1/√ λ = 2.0log(Re √ λ)-0.8 ・・・(4)-3
이 식은, 광범위한 Re에서 실험 결과와 일치하지만, λ가 Re의 단순한 함수가 아니기 때문에 다루기가 어렵습니다.
관내벽면의 거칠기가 무시할 수 없는 크기인 경우는, 상대 거칠기 ε/d의 함수로서 관마찰계수 λ를 취급할 필요가 있습니다. 상대 거칠기는, 튜브의 내부 직경 d에 대한, 벽면의 평균 거칠기 ε의 비율입니다.
각종 실험 결과로부터는, 어느 레이놀즈수를 넘으면 관마찰계수 λ는 레이놀즈수에 의하지 않고, 상대 조도 ε/d마다 일정치가 되는 경향을 나타냅니다.
λ=1/{1.14-2.0log(ε/d)}2 ・・・(5)
각종 공업에서 실용적으로 사용되고 있는 관에 대해, 상대 거칠기 ε/d, 레이놀즈수 Re, 관마찰계수 λ의 관계를 근사적으로 나타내는 식으로서, 다음과 같은 콜브룩의 식이 있습니다.
1/√λ=-2log((ε/d)/3.71+2.51/(Re√λ)) ・・・(6)
어느 정도 레이놀즈수가 큰 영역에서 실용적으로는, 관의 재질이나 제조법으로부터 정해지는 평균 조도와 직경으로부터 상대 조도를 구해, (6)식을 로그 그래프에 정리한 무데이 선도라고 불리는 그림 등을 기본으로 λ를 일정값으로 판독하여, (2)식에 의해 직관손실헤드를 구합니다.
단, 경년적으로 관내벽이 녹이나 부식으로 거칠어지면, 상대 거칠기가 커져서 관마찰계수 λ도 증대하므로, 무데이 선도에서 판독한 값에 대해 여유를 예상한 값을 이용하여 손실 계산합니다.
λ가 일정한 경우, 직관의 손실 헤드는 (2)식보다 길이 직경비와 유속의 제곱에 비례합니다.
3. 관로 단면이 비원형일 경우
각종 산업이나 건축 설비에 이용되는 관로에는, 직사각형 등 단면이 비원형인 형상인 것도 있습니다.
이 경우는, 다음 식으로 정의되는 수력 직경 dh를 이용하여 (1)의 레이놀즈 수, (2)의 다르시・와이스바흐의 식에 의한 직관 마찰 손실이나 상대 거칠기(상대조)를 계산합니다.
dh=4A/S ・・・(7)
A는 관로의 단면적, S는 젖은 가장자리 길이라고 부르며, 관로 단면의 주위 길이를 맣합니다. (원형 단면이면 dh = 4 x πd2/4/(πd) = d가 됩니다.)
또한 A/S를 수력 평균 깊이 라고 합니다.
4. 각종 관로 요소의 손실
실제의 배관 계통에는, 직관 이외의 다양한 관로 요소(굽힘, 확대, 축소, 밸브 등)가 존재하고, 이들 관로 요소에 있어서 단면 형상이나 방향 변화에 기인하는 압력 손실이 발생합니다 .
관로 요소에 대한 손실 헤드를 hs라고 하면
hs=ζv2/2g ・・・(8)
ζ (제타) : 손실 계수 ... 관로 요소의 종류와 형상모양에 의해 결정됩니다.
v(m/s) : 관로 요소의 유속. 확대나 축소 등 유속이 변화하는 경우는 빠른 측의 유속을 취합니다.
(8)식에서 관로 요소에 있어서의 손실 헤드는, 직관과 마찬가지로 유속의 제곱에 비례하는 것을 알 수 있습니다.
ζ에 대해서는 각 요소의 형상 마다 자료에서 구합니다.
여기에서는 그 일부를 소개합니다.
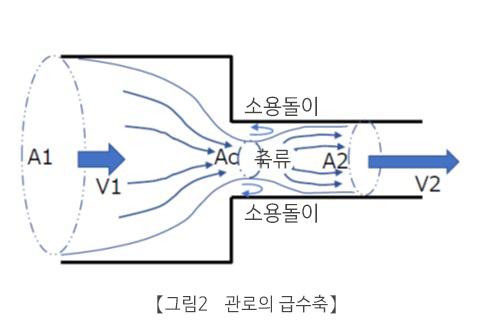
(1)관로의 급 수축
그림2와 같이, 관로 단면적이 급격히 좁아질 때, 흐름 관성 때문에 급 축소 코너부 바로 다음에, 흐름은 관로 면적보다 좁아(가늘어)집니다. 이것을 "축류"라고 합니다.
그 후 흐름은, 관로 가득 퍼져 흐르게 되지만, 이 때 흐름의 확대에 따른 소용돌이가 발생하여 의해 손실이 생깁니다.
가는 관로 가득 퍼져 흐를 때의 유속을 V2, 가는 관로 단면적을 A2, 축류부의 유로 단면적을 Ac로 하면,
손실 계수 ζ=(A2/Ac-1)2=(1/Cc-1)2 ・・・(9)
손실 헤드 hs=ζV22/2g=(1/Cc-1)2V22/2g ・・・(10)
로 됩니다.
(9)(10)식의 “Cc”는 수축 계수라고 불리며, 굵은 관로 단면적을 A1로 했을 때, 단면적비 A2/A1에 대한 Cc, ζ의 값은 아래
표와 같습니다.
【표:급 수축관의 손실 계수(기계 공학 편람으로부터)】
| A2/A1 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 11 |
| Cc | 0.61 | 0.62 | 0.63 | 0.65 | 0.67 | 0.70 | 0.73 | 0.77 | 0.84 | 1/00 |
| ζ | 0.41 | 0.38 | 0.34 | 0.29 | 0.24 | 0.18 | 0.14 | 0.089 | 0.036 | 0 |
2) 탱크에서 관로로의 입구
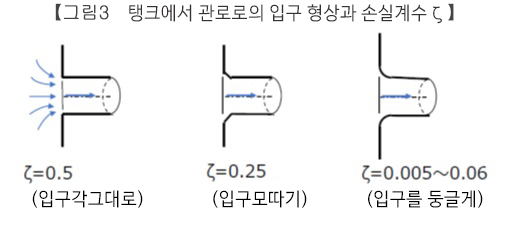
급 축소로, 굵은 쪽의 관로 단면적이 매우 큰, 즉 A1=∞, A2/A1=0의 경우에 해당하지만, 입구부의 형상에 따라 손실 계수가 달라집니다
그림3과 같이, 입구부를 둥글게 함으로써, 각부 그대로의 상태에 비해 손실 계수를 0.1~0.01배 정도로 작게 할 수 있습니다.
(3)관로의 급확대
그림 4와 같이 관로 단면적이 급격히 확대되는 곳에서는, 흐름이 박리되면서 발생하는 소용돌이에 의한 손실이
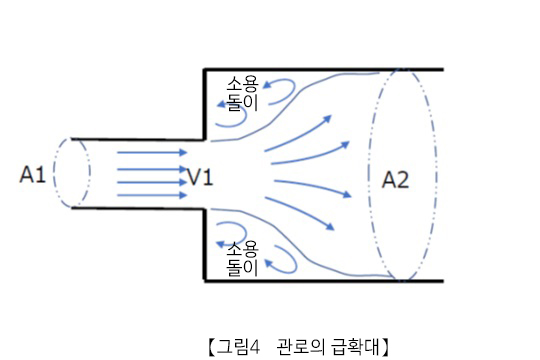
발생합니다.
가는 관의 단면적을 A1, 확대관의 단면적을 A2로 하면, 급확대의 손실 계수는 다음 식으로 계산됩니다.
ζ=ξ(1-A1/A2)2 ・・・(11)
빠른 측(가는 관)의 유속을 V1이라고 하면, 급확대에 의한 손실 헤드는
hs=ζv2 /2g=ξ(1-A1/A2)2 x V12 /2g ・・・(12)
ξ(구자이)는 보정 계수로 0.93~1.08의 값이 됩니다.
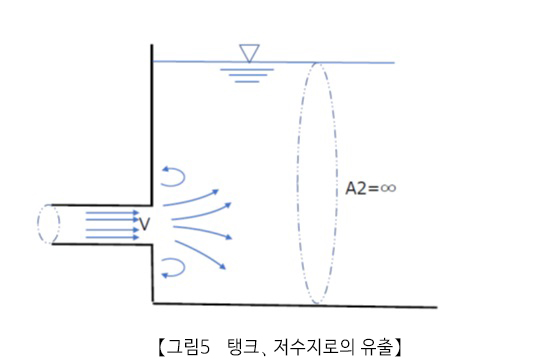
(4)관로에서 저수지나 탱크로의 유출
그림5와 같은 경우는, (3)의 관로 급 확대로, 확대관의 단면적이 매우 큰, 즉 (11)식에서 A2=∞로 간주합니다.
보정 계수 ξ=1.0 으로 ζ=1.0 이 됩니다.
hs=ζv2/2g=v2/2g
즉, 관로 내의 속도 수두=유출에 있어서의 손실 헤드가 됩니다.
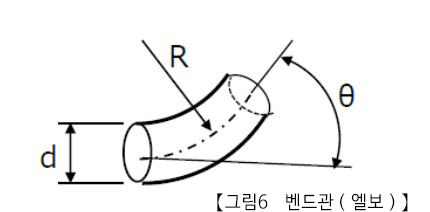
(5)굴곡부 (구브러진 부분)
그림 6과 같이 곡률 반경 R로 구부러지는 관로 요소를 벤드라고합니다.
벤드의 손실 계수에 대해서는 실험 결과에 근거한 (13)식과 같은 와이스바흐의 근사식이라고 하는 식이 있습니다.
ζ=(0.131+0.1632(d/R)3.5)(θ/90) ・・・(13)
관경 d에 대한 굽힘 반경 R을 크게할수록, 굽힘 각도 θ가 작게 할수록, 손실은 작아집니다. (13)식의 적용 범위는 d/R=0.4~2.0입니다.
덧붙여, 시판의 배관 피팅에는 형상은 벤드 라도 「엘보」라고 부르는 것이 많습니다.
이러한 시판품 엘보에는 R의 큰 “롱 엘보” 와 R의 작은 “쇼트 엘보”가 있으며, 구부러진 각도에 대해서는 θ=90°의 것이나 45°의 것이 있습니다.
롱 엘보가 손실이 적지 만 배관 공간에 따라 설치되지 않을 수 있습니다. 또한 롱 엘보는 쇼트 엘보 보다 무게가 크고 가격은 비싸 집니다.
예산이나 배관계획에 지장이 없는 범위에서, 손실이 적은 롱엘보를 사용하도록 합니다.
(6)밸브
한 예를 들면, 구경 25mm의 Gate Valve and Ball Valve 의 전개시에 있어서의 손실 계수를 비교하면, Gate Valve 0.233, Ball Valve 6.09와 매우 큰 차이가 있습니다.
Ball Valve 는, 전폐시의 누설을 제로로 할 수 있고, 유량의 미세 조정도 가능하다는 등의 이점이 있습니다만, 너무 많이 사용하면 손실이 커집니다.
예를 들어, 어떤 유체 기기에 출입하는 배관의 입구측을 Gate Valve, 출구측을 Ball Valve 하는 등, 기능과 손실을 모두 고려한 선택을 실시하도록 합니다.
직관 손실hL과 관로 요소의 손실hs를 합계함으로써, 어느 유량의 유체를 배관으로 이송할 때에 필요한 유체기계의 성능사양(펌프라면 전양정)을 계산할 수 있습니다.
연속의 식으로부터, 유량이 일정하면 배관 직경을 크게 할수록 유속이 작아지므로 압력 손실을 작게, 즉 필요한 유체 기계의 성능 사양을 저감할 수 있습니다.
그러나, 배관 직경을 높임으로써 유체 기계나 밸브 등의 구경도 커져 코스트 업(비용상승)으로 이어질 수도 있습니다.
성능 사양 저감 효과(런닝 코스트 다운)와 구경 업에 의한 이니셜 코스트 업 영향의 양면으로부터 검토를 실시해, 최적의 관경을 선택하도록 합시다.
| ============================================================================= |
O-TRAP 관련 홈페이지 : http://k.o-trap.cn
O-TRAP 관련 E-mail 문의처 : tjchung@naver.com
tjchung@hanmail.net
O-TRAP 관련 Tel 문의처 : 070-7747-8290
'스팀트랩(드레인배출기,O-Trap)' 카테고리의 다른 글
| 증기배관을 장기간 정지할 때, 증기 배관 관리 (0) | 2021.12.09 |
|---|---|
| 증기 시스템 솔루션 에 대한 종합 설명 (0) | 2021.11.29 |
| 배관 압력 손실 계산 방법 (5) | 2021.11.20 |
| 증기 사용하여 플라스틱 압출, 고무나 플라스틱 성형하는 금형에서 응축수를 배출시키는 스팀트랩(O-TRAP)의 중요성 및 금형온도조절계통 참고도 (0) | 2021.11.02 |
| 고정오리피스식 스팀트랩(O-TRAP) 표준형 설치 사례 (0) | 2021.09.16 |